网址：https://ww2.mathworks.cn/help/signal/ug/dct-for-speech-signal-compression.html
描述：本案例由1个示例构成

-

针对以上案例，采用Python语言实现。

-

加载一个包含“强”这个词的文件，这个词是由一个女人和一个男人说的。信号在8 kHz处采样。 利用离散余弦变换对女性语音信号进行压缩。将信号分解为DCT基向量。 分解中的术语和信号中的样本一样多。矢量展开系数X测量每个组件中存储了多少能量。将系数从最大到最小排序。 并且找出多少DCT系数代表99.9%的能量在信号中。将数字表示为总数的百分比。 分解中的术语和信号中的样本一样多。矢量展开系数X测量每个组件中存储了多少能量。将系数从最大到最小排序。

from scipy.io import loadmat
from scipy.fft import dct,idct
import numpy as np
import matplotlib.pyplot as plt
m=loadmat("strong.mat")
x=m['her']
x=x.reshape(-1,1)
X=dct(x,norm='ortho')
X=X.reshape(len(X))
XA=abs(X)
XX=sorted(XA,reverse=True)
ind=sorted(range(len(X)), key=lambda k: XA[k])
need=1
while np.linalg.norm(X[ind[1:need+1]])/np.linalg.norm(X)<0.999:
  need = need+1
xpc = need/len(X)*100
X[ind[need+1:]]=0
xx=idct(X)
plt.plot(x)
plt.plot(xx)
plt.plot(x-xx)
plt.legend(["Original","45% of coeffs","Differences"])
plt.show()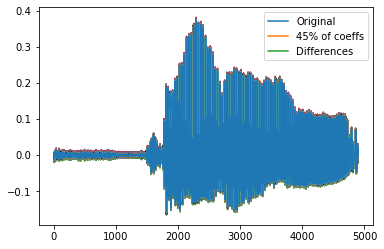

重复分析男性的声音。找出多少DCT系数代表99.9%的能量，并表示数字为一个百分比的全部。 将其余的系数设置为零，并从压缩版本重构信号。绘制原始信号，其重构，以及两者之间的区别。

from scipy.io import loadmat
from scipy.fft import dct,idct
import numpy as np
import matplotlib.pyplot as plt
m=loadmat("strong.mat")
y=m['him']
y=y.reshape(-1,1)
Y=dct(y,norm='ortho')

Y=Y.reshape(len(Y))
YA=abs(Y)
YY=sorted(YA,reverse=True)
ind=sorted(range(len(Y)), key=lambda k: YA[k])
need=1
while np.linalg.norm(Y[ind[1:need+1]])/np.linalg.norm(Y)<0.999:
  need = need+1
ypc=need/len(Y)*100
Y[ind[need+1:]]=0
yy=idct(Y)
plt.plot(y)
plt.plot(yy)
plt.plot(y-yy)
plt.legend(["Original","57% of coeffs","Differences"])
plt.show()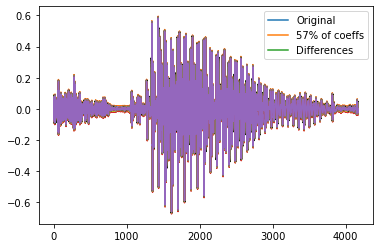

在这两种情况下，大约一半的DCT系数足以合理地重建语音信号。如果所需能量分数为99%，所需系数的数目将减少到总能量的20%左右。重建的结果是低劣的，但仍然是可理解的。 对这些和其他样本的分析表明，需要更多的系数来表征男人的声音，而不是女人的声音。